Notícias
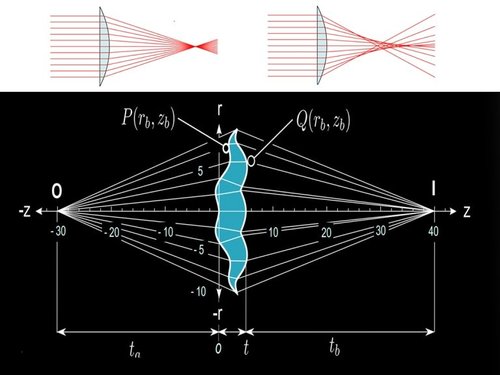
Aberração esférica
Um trio de físicos mexicanos resolveu um problema óptico que permaneceu sem solução por 2.000 anos.
E, ao solucionar o quebra-cabeças, eles abriram a possibilidade de criação de lentes de formato livre que poderão encontrar aplicações em todos os campos da óptica, de óculos e microscópios a telescópios.
Mais de 2.000 anos atrás, o matemático grego Díocles identificou um problema com as lentes: Ao olhar através de dispositivos equipados com elas, as bordas pareciam mais difusas do que o centro. Ele propôs que o efeito ocorre porque a luz atingia as lentes esféricas em um ângulo que não poderia ser focado por causa das diferenças na refração. Esse problema, que passou a ser conhecido como aberração esférica, resistiu a todas as tentativas de solução, incluindo as de Isaac Newton e de Gottfried Leibniz.
Em 1949, Gerhard Wassermann e Emil Wolf criaram um meio analítico para descrever o problema, que passou então a ser conhecido como o problema Wasserman-Wolf. Eles sugeriram que a melhor abordagem para resolver o problema seria usar duas superfícies adjacentes asféricas para corrigir as aberrações - uma lente asférica é uma lente cujos perfis de superfície não são partes de uma esfera ou cilindro.
Desde aquela época, pesquisadores e engenheiros criaram uma variedade de maneiras de resolver o problema em aplicações específicas, principalmente em câmeras e telescópios. A maioria desses esforços envolve a criação de lentes asféricas para neutralizar os problemas de refração. E, embora tenham resultado em melhorias, as soluções geralmente são caras e inadequadas para algumas aplicações.

Solução da aberração esférica
Continua depois da publicidade |
Agora, Rafael González-Acuña e seus colegas da Universidade Nacional do México e do instituto Tecnológico de Monterrey descobriram um meio para corrigir o problema com lentes de qualquer tamanho.
Expressa em uma longa fórmula matemática, a solução baseia-se em moldar a forma de uma segunda superfície asférica, precisamente projetada para interagir com a superfície da lente original. Essa segunda superfície corrige as distorções geradas pela primeira, resultando na eliminação da aberração esférica.
Os pesquisadores mexicanos testaram sua solução em simulações computadorizadas, mostrando que uma lente biasférica pode alcançar uma precisão de 99,999999999%.
Eles sugerem que a fórmula pode ser usada em aplicações como óculos, lentes de contato, telescópios, binóculos e microscópios.
Gostou? Então compartilhe:
